1.6 KiB
1.6 KiB
Digital Audio Processing
Analysis and manipulation of PCM Audio.
Sine Wave
import numpy as np
samplerate = 44100
frequency = 440
samples = 44100
x = np.arange(samples)
return 100 * np.sin(2 * np.pi * frequency * x / samplerate)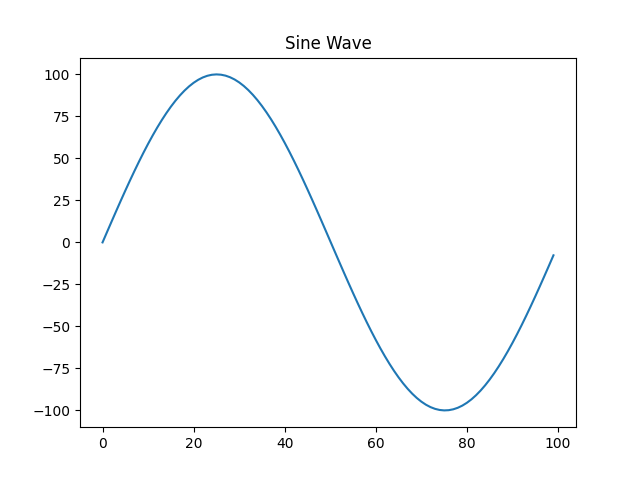
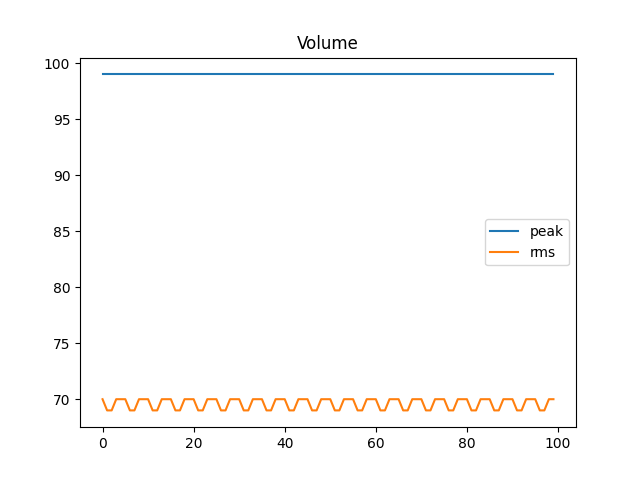
Getting volume with audioop
The power of an audio signal is computed using the root mean square of the fragment:
\begin{equation} {\displaystyle x_{\text{RMS}}={\sqrt {{\frac {1}{n}}\left(x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\right)}}.} \end{equation} import audioop
import struct
from matplotlib import pyplot as plt
def sinewave():
<<sine-wave>>
wave = sinewave()
chunksize = 441
chunks = [wave[i : i + chunksize] for i in range(0, len(wave), chunksize)]
raw_chunks = [struct.pack(f"{chunksize}h", *map(int, chunk)) for chunk in chunks]
plt.plot(
[audioop.max(c, 2) for c in raw_chunks],
label="peak")
plt.plot(
[audioop.rms(c, 2) for c in raw_chunks],
label="rms")
plt.legend()
plt.title("Volume")
plt.savefig("dap-volume.png")
return "dap-volume.png"